- 이번 포스팅으로는 배열 내의 데이터들을 순서대로 정렬하는 효율적인 방식인 정렬 알고리즘을 정리할 것입니다.
소프트웨어 공학 범위에서 배우는 기본 필수적으로 알아야 하는 마지막 알고리즘의 이론입니다.
정렬 알고리즘의 실제 구현은 하지 않으며, 나중에 C 언어로 따로 구현글을 정리할까 합니다.
- 정렬이란, 다수의 데이터를 일정한 규칙에 따라 순서대로 나열하는 방법입니다.
작거나 앞선 데이터를 시작으로 점차 데이터가 커지는 방향으로 정렬하는 오름차순(Ascending Order) 정렬과,
크거나 뒷선 데이터를 시작으로 점차 데이터가 작아지는 방향으로 정렬하는 내림차순(Descending Order) 정렬이 있습니다.
[정렬의 종류]
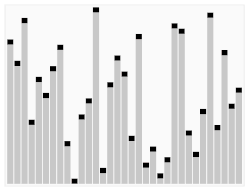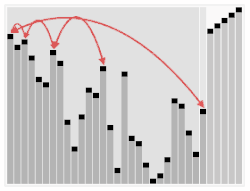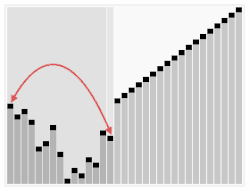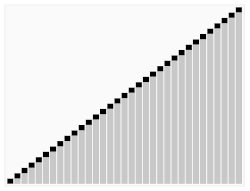
(선택(Selection) 정렬)
- 시간 복잡도
평균 : O(N^2)
최악 : O(N^2)
정렬 대상 중 기준값으로 선택된 데이터를 나머지 데이터와 비교하는 정렬 방식입니다.


- 프로세스
1. 현재 위치의 데이터를 기준으로 선택
첫 번째 인덱스(0번)부터 시작해서, 현재 위치의 데이터를 기준으로 함.
2. 오른쪽에 있는 데이터 중에서 가장 작은 값 찾기
현재 위치 다음 인덱스부터 끝까지 반복하며 최솟값의 위치를 찾음.
3. 최소값과 현재 위치의 데이터 교환
찾은 최솟값이 현재 위치의 값보다 작으면, 두 값을 서로 교환(swap).
4. 다음 인덱스로 이동하며 반복
현재 위치를 오른쪽으로 한 칸 옮겨가며 위 과정을 반복.
리스트 끝에서 두 번째 인덱스까지 반복하면 정렬 완료.
- 특징 : 최소 데이터가 배열에서 왼쪽으로 차곡차곡 쌓여가며 정렬되는 형태입니다.
(버블(Bubble) 정렬)
- 시간 복잡도
평균 : O(N^2)
최악 : O(N^2)

- 프로세스
1. 배열의 처음부터 시작
인접한 두 개의 데이터를 비교합니다.
2. 두 데이터를 비교하여 순서가 잘못되었으면 교환
앞의 값이 뒤의 값보다 크면 두 값을 서로 교환(swap)합니다.
(오름차순 정렬 기준)
3. 끝까지 한 번 반복하면 가장 큰 값이 맨 끝으로 이동
이렇게 한 번 반복을 하면 가장 큰 값이 배열의 가장 뒤로 "버블처럼" 올라갑니다.
4. 다음 반복에서는 마지막 위치를 제외하고 반복
이미 정렬된 마지막 요소는 제외하고 반복합니다.
이 과정을 배열의 크기 - 1번 반복하면 정렬 완료!
- 특징 : 앞서 설명했듯 큰 값이 배열 뒤쪽으로 차곡차곡 버블처럼 올라서 쌓여가는 형태입니다.
최대 값을 위로 올리고, 다음에는 최소 값을 아래로 내리고, 다시 최대 값을 위로 올리고...
이런식으로 버블 정렬 방식대로 방향을 좌우로 번갈아 이동시키는 칵테일 정렬 방식도 있습니다.

(삽입(Insertion) 정렬)
- 시간 복잡도
평균 : O(N^2)
최악 : O(N^2)


- 프로세스
1. 두 번째 요소부터 시작
현재 요소를 기준으로, 왼쪽에 있는 정렬된 부분과 비교합니다.
2. 왼쪽 정렬된 부분과 비교하여 삽입 위치 탐색
현재 요소가 왼쪽의 어떤 요소보다 작으면, 해당 요소 뒤로 밀고 빈 자리에 현재 값을 삽입합니다.
만약 비교하다가 현재 요소보다 작은 값이 왼쪽에 있는게 보이면 그자리에서 비교를 멈출 수 있습니다.
3. 정렬된 범위를 한 칸씩 확장
반복하면서 정렬된 범위를 하나씩 확장해 나갑니다.
4. 마지막 요소까지 위 과정을 반복하면 정렬 완료
리스트가 끝날 때까지 위 과정을 반복하면 정렬이 완료됩니다.
- 특징 : 비교 인덱스를 좌측 배열에 본인이 위치해야할 곳으로 삽입하는 개념의 정렬입니다.
(쉘(Shell) 정렬)
- 시간 복잡도
평균 : O(N^1.5)
최악 :O(N^1.5)

- 설명
많은 데이터의 이동이 필요한 삽입 정렬의 단점을 보완한 방식입니다.
데이터의 간격을 정하고, 간격을 점차 줄여가면서 삽입 정렬을 진행하는 정렬입니다.
간격을 설정할 때의 기준은,
(1.72)^3 * sqrt(N)
으로 하는 것이 좋고,
데이터 수가 적거나 보편적 상황에서는 N/2 로 정합니다.
- 프로세스
[78, 68, 87, 93, 46, 54, 39, 14, 86, 37, 50]
위 배열을 가지고 설명하겠습니다.
1. 간격을 정하기 : 배열 개수가 11개이므로, 간단히 2로 나누어서 몫인 5를 간격으로 정함
2. 간격만큼 그룹화 : 78 부터 시작해서 5간격 뒤의 54, 거기서 5간격 뒤의 50
[78,54,50]
78 뒤에서부터 54 이전까지 위와 같은 작업을 반복해서,
[69,39]
[87,14]
[93,86]
[46,37]
이렇게 그룹화 합니다. (그룹화는 실제로 배열을 쪼개는 것이 아니라 그룹화한 인덱스를 기록해두는 것입니다.)
3. 각 그룹별 삽입 정렬을 수행 :
[50,54,78]
[39,69]
[14,87]
[86,93]
[37,46]
인덱스 기반으로 삽입 정렬을 수행했으므로,
[50,39,14,86,37,54,69,87,93,46,78]
위와 같은 상태입니다.
4. 간격을 1/2 로 줄이기 : 5의 간격이었으므로 반으로 나눈 몫인 2의 간격으로 진행합니다.
5. 새 간격만큼 그룹화 :
50 부터 시작해서 2간격 뒤의 14, 거기서 2 간격 뒤의 37, ... 이렇게 반복해서
[50,14,37,69,93,78]
50 뒤에서부터 14 이전인 39 에서 시작해서 위와 같은 작업을 반복해서,
[39,86,54,87,46]
이상입니다.
6. 새 그룹별 삽입 정렬을 수행 :
[14,37,50,69,78,93]
[39,46,54,86,87]
위와 같이 삽입 정렬을 해서 아래와 같은 상태입니다.
[14,39,37,46,50,54,69,86,78,87,93]
7. 간격이 1이 될 때까지 위 과정을 반복하고, 간격이 1이 되면 전체 삽입 정렬 수행 :
이제 간격 2에서 1/2 를 해서 간격이 1이 되었으므로, 전체 데이터를 대상으로 삽입 정렬을 진행하면 끝입니다.
- 삽입 정렬은 진행될수록 좌측이 쌓이고, 그렇기에 비교 횟수도 늘어날수 있습니다.
쉘 정렬은, 구간을 나누어 삽입 정렬을 수행함으로써 좌측이 쌓이기 전에 그룹별 정렬을 시킬 수 있으며,
최종적으로 전체 삽입정렬을 할 시점에는 어느정도 전체 배열이 정렬된 상태이므로 그만큼 비교 연산을 덜 해도 된다는 이점으로 삽입 정렬의 문제점을 해소하였습니다.
(힙(Heap) 정렬)
- 시간 복잡도
평균 : O(NlogN)
최악 : O(NlogN)
- 정리
정렬 대상을 완전 이진 트리의 일종인 Heap 의 형태로 만들어 정렬하는 방식입니다.
Heap 은 최대 힙과 최소 힙의 종류가 있으며, 각각 최대 값, 혹은 최소값이 루트 노드에 위치합니다.
힙 정렬은 배열을 이러한 힙 형태로 만들고, 루트에 위치한 최대, 최소값을 하나씩 정렬 배열에 쌓아가는 방식으로 동작합니다.
- 프로세스
먼저 최대 힙에 데이터를 입력하는 방법부터 알아보겠습니다.
[50,69,41,94,53,58]
이런 배열을 차례로 최대 힙으로 입력하는 과정을 보겠습니다.
1. 처음 50 삽입
50
2. 69 삽입 :
완전 이진 트리는, 부모 -> 좌측 -> 우측 순으로 채워나가므로, 50의 좌측으로 입력합니다.
그런데, 69는 현재 부모로 있는 50 보다 크기 때문에 둘을 바꿔줍니다.
69
/
50
3. 41 삽입 :
69 보다 작으니 우측 자식으로 넣습니다.
69
/ \
50 41
4. 94 삽입 :
원래는 50의 좌측 자식으로 넣습니다.
그러나 50보다 크기 때문에 둘을 바꿉니다.
또한 69 보다 크기 때문에 이것도 바꿉니다.
94
/ \
69 41
/
50
5. 53 삽입 :
69 보다 작으니 그대로 비어있는 우측 자식으로 넣습니다.
94
/ \
69 41
/ \
50 53
6. 58 삽입 :
41 의 좌측 자식으로 넣지만, 41 보다 크기 때문에 자리를 바꿉니다.
94
/ \
69 58
/ \ /
50 53 41
7. 최대 힙이 준비되었으므로 이를 배열에 넣고 힙에서 제거합니다.
[..., 94]
최대 힙의 루트 노드는 최대값이므로 이 값을 배열의 오른쪽으로 채워넣고,
힙의 마지막 레벨의 가장 우측의 단말노드를 비어있는 루트 노드 위치로 이동시킵니다.
41
/ \
69 58
/ \
50 53
이런 상태가 될 것인데, 최대 힙이 아니게 되었으므로 최대 힙 성질을 복구시켜야 합니다.
8. 수정된 부분은 뿌리 노드 뿐입니다.
힙의 특성상 트리의 레벨별 계층 구조가 유지됩니다.(분기별 하위 레벨의 어느 값도 상위 레벨의 값보다 클 수 없습니다.)
고로 좌우를 살펴보며 큰 값과 교체해나가기만 하면 됩니다.
41의 좌우 자식을 보면 69 가 크기 때문에 41 은 69 와 위치를 바꿉니다.
다시, 41 의 좌우 자식을 보면 53 이 가장 크기 때문에 41 과 53 의 자리를 바꿉니다.
69
/ \
53 58
/ \
50 41
9. 다시 정렬된 최대 힙에서 루트를 배열로 뺍니다.
[..., 69, 94]
그리고 가장 끝 단말인 41 을 다시 루트로 둡니다.
10. 이제 8번부터 계속 반복하면 됩니다.
(이진 병합(Merge) 정렬)
- 시간 복잡도
평균 : O(NlogN)
최악 : O(NlogN)

- 설명
두 데이터를 한쌍으로 병합하여 정렬하고, 정렬된 두 그룹을 다시 한쌍으로 하여 정렬하는 것을 반복하는 방식입니다.
- 프로세스
[6,5,3,1,8,7,2,4]
위 배열을 기준으로 설명하겠습니다.
1. 위 배열을 모두 잘개 쪼갭니다.
6 5 3 1 8 7 2 4
2. 두개씩 비교를 해서 정렬하며 묶습니다.
[5,6] [1,3] [7,8] [2,4]
3. 두 그룹을 비교해서 정렬하며 묶습니다.
각 그룹간 비교 및 정렬시에는 그룹간 최소 데이터를 비교하며 정렬 배열에 넣는 것입니다.
[5,6] 의 최소는 5, [1,3] 의 최소는 1 이므로, 1을 먼저 넣고,
[5,6] 의 최소는 5, [3] 의 최소는 3 이므로 3을 넣는 식으로 진행합니다.
결과,
[1,3,5,6] [2,4,7,8]
이 됩니다.
4. 병합된 그룹을 또 3번과 같이 병합하며, 그룹이 마지막 1개가 될 때 까지 반복하면 됩니다.
(버킷(Bucket) 정렬)
- 시간 복잡도
평균 : O(D+N)
최악 : O(N^2)


- 정보
정렬 대상의 데이터 범위를 균등하게 나눈 여러 버킷을 생성하여 정렬하는 정렬 알고리즘입니다.
고로 데이터 범위의 파악이 가능해야합니다.
- 프로세스
[14,2,7,5,13,9,15,4,20,12,6]
위 배열로 설명하겠습니다.
보시다시피 데이터는 11개이며, 버킷 정렬을 할 때 필요한 데이터의 범위는 1 에서 20까지 인 것을 알 수 있습니다.
데이터 범위를 5단위로 나누어 4개의 버킷을 만드는 것으로 결정하겠습니다.
1~5 버킷, 6~10 버킷,11~15 버킷, 16~10 버킷입니다.
1. 배열을 순회하며 버킷에 데이터를 입력합니다.
14는 11~15 버킷으로, 2는 1~5 버킷으로... 이런식으로 데이터를 각 버킷에 입력합니다.
1~5 버킷 : [2,5,4]
6~10 버킷 : [7,9,6]
11~15 버킷 : [14,13,15,12]
16~20 버킷 : [20]
2. 각 버킷별 삽입 정렬 등 별도 정렬 알고리즘으로 정렬합니다.
[2,4,5]
[6,7,9]
[12,13,14,15]
[20]
3. 버킷별 정렬된 리스트를 범위 순서대로 전부 합칩니다.
[2,4,5,6,7,9,12,13,14,15,20]
(퀵(Quick) 정렬)
- 시간 복잡도
평균 : O(NlogN)
최악 : O(N^2)
- 설명
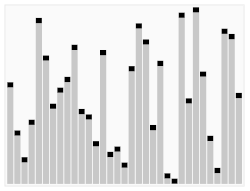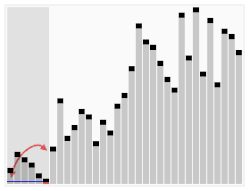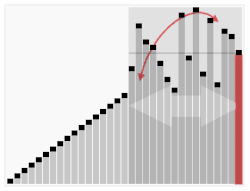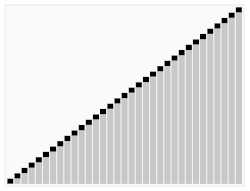
기준 값(pivot)을 하나 정해서 작은 값은 왼쪽, 큰 값은 오른쪽으로 나누고 각 부분 배열을 재귀적으로 정렬하는 분할 정복 기반 정렬입니다.
- 프로세스
[56, 33, 87, 41, 99, 13, 67, 27, 73]
위 배열을 기준으로 설명하겠습니다.
1. 첫번째 피벗 선택
일단 맨 앞 요소(56) 를 피벗으로 선택하겠습니다.
(※ 퀵정렬은 피벗 선택 방식이 다양합니다 – 여기선 가장 단순한 방식 사용)
피벗: 56
→ 56보다 작은 값들: [33, 41, 13, 27]
→ 56보다 큰 값들: [87, 99, 67, 73]
[작은 쪽 정렬] + [피벗] + [큰 쪽 정렬]
= [33, 41, 13, 27] + [56] + [87, 99, 67, 73]
2. 왼쪽 그룹 정렬
피벗: 33
→ 33보다 작은 값: [13, 27]
→ 33보다 큰 값: [41]
[13, 27] + [33] + [41]
3. [13, 27] 정렬
피벗: 13
→ 작은 값: 없음
→ 큰 값: [27]
[13] + [27] = [13, 27]
→ 왼쪽 그룹 전체 정렬 완료:
[13, 27, 33, 41]
4. 오른쪽 그룹 정렬 [87, 99, 67, 73]
피벗: 87
→ 작은 값: [67, 73]
→ 큰 값: [99]
[67, 73] + [87] + [99]
5. [67, 73] 정렬
피벗: 67
→ 작은 값: 없음
→ 큰 값: [73]
[67, 73]
→ 오른쪽 그룹 전체 정렬 완료:
[67, 73, 87, 99]
6. 최종 정렬 단계 조합
왼쪽: [13, 27, 33, 41]
피벗: 56
오른쪽: [67, 73, 87, 99]
[13, 27, 33, 41, 56, 67, 73, 87, 99]
- 요약하자면,
1. 기준(pivot) 하나 정함
2. 피벗보다 작은 값/큰 값으로 분할
3. 재귀 호출로 왼쪽, 오른쪽 각각 정렬
4. 병합이 아닌 연결로 정렬이 완성됨
입니다.
- 퀵정렬의 특징은, 분할 정복 구조이므로,
좌우로 나뉘어진 배열에 대해 독립적으로 정렬이 진행되기에 이를 병렬로 처리할 수도 있습니다.
고로 연산량이 줄어들지는 않지만, 좌우 동시 처리로 인하여 연산 속도 향상 효과를 볼 수 있습니다.
(스레드/프로세스 생성 비용(콘텍스트 스위칭으로 인한 오버헤드 및 처리 속도 저하)이 있으므로 너무 작은 배열까지 전부 병렬처리시에는 오히려 느려질 수 있으므로 적절한 횟수만 병렬처리를 하도록 처리하세요.)
'Study > Computer Science' 카테고리의 다른 글
| [정보 처리] 11. 제품 소프트웨어 패키징 (0) | 2025.04.14 |
|---|---|
| [정보 처리] 10. 시스템 통합 구현 (0) | 2025.04.13 |
| [정보 처리] 8. 탐색 알고리즘 이론 (0) | 2025.04.12 |
| [정보 처리] 7. 자료구조 이론 (0) | 2025.04.11 |
| [정보 처리] 6. 공학적 응용 소프트웨어 설계 방식 (0) | 2025.04.10 |
