- 먼저 좌표계에 대해 알아봅시다.

좌표계란, 공간에서 점의 위치를 나타내는 데이터인 좌표를 나타내는 방식을 정의한 체계를 의미하며,
평면상의 점을 정의하는 가장 기본적인 방법을 사용하는 직교 좌표계(Cartesian Coordinate System), 반지름, 극각, 방위각으로 점을 정의하는 구면 좌표계(Spherical Coordinate System) 등의 좌표계가 있습니다.
구면 기하학을 기반으로 하여 지구의 곡면에서 점의 위치를 위도와 경도로 정의하는 좌표계가 바로 지리적 좌표계 (Geographic Coordinate System) 입니다.
GPS 시스템, 지도, 내비게이션 등에서 위치 정보를 표현할 때 사용됩니다.
지리적 좌표계에서의 좌표에 대해 알아봅시다.
위도와 경도로 이루어진 지도 좌표란, 2차원 좌표 체계와는 다르게 지구라는 구의 특정 기준에서 부터 특정 위치까지의 각도를 나타내는 정보입니다.
위도는 지구의 적도를 기준으로 북쪽 혹은 남쪽으로 얼마나 떨어져 있는지를 나타내는 값으로, 0 에서 90 까지의 범위를 가지고 있습니다. 적도를 0으로 하여, 북쪽 끝을 북위 90도라고 부르며, 남쪽 끝을 남위 90도라고 부릅니다.
경도란 영국의 옛 그리니치 천문대(Royal Observatory, Greenwich)의 위치에서 기원한 본초 자오선(Prime Meridian)를 기준으로 하여 동과 서를 나누는 가상의 선을 만들어놓고, 이를 기준으로 하여 서쪽으로 180도, 동쪽으로 180도까지의 범위를 가지고 있습니다.
본초 자오선을 0으로 두었을 때, 서쪽으로 본초 자오선의 맞은편에 있는 위치를 서경 180도라고 부르고, 동쪽으로 본초 자오선의 맞은편에 있는 위치를 동경 180 도라고 부릅니다.
동경과 서경이 마주하는 이 180도 지점이 바로 날짜가 변경되는 선입니다.
- 지리적 좌표계는 지구의 표면에서 위치를 정의하는 다양한 하위 시스템을 포함합니다.
1. WGS84 (World Geodetic System 1984)
2. NAD83 (North American Datum 1983)
3. ED50 (European Datum 1950)
4. GDA94 (Geocentric Datum of Australia 1994)
5. CGCS2000 (China Geodetic Coordinate System 2000)
6. ITRF (International Terrestrial Reference Frame)
7. EPSG:4326
8. OSGB36 (Ordnance Survey Great Britain 1936)
9. JGD2000 (Japanese Geodetic Datum 2000)
10. MGRS (Military Grid Reference System)
등의 시스템이 존재하며,
각 시스템의 존재 의의는 각 국가별 좌표 계산의 정밀도를 올리기 위한 시스템입니다.(어떤 지형은 높이 솟아있고, 어떤 지형은 울퉁불퉁하고, 어떤 지형은 비틀어져 있는 등의 지역별 오차에 최적화된 시스템)
이 중 글로벌하게 대표적으로 사용되는 WGS84 좌표계만 간단히 알아보자면,
지구의 타원체 모델을 기반으로 하며, 위도와 경도를 사용하여 위치를 정의하며 GPS, GIS, 지도 제작 등에서 표준으로 사용되는 시스템이라는 것만 알아둡시다.
이에 대한 자세한 공부 및 정리는 추후 게시글로 올리겠습니다.
또한, 위에서 설명한 지리적 좌표계를 제외한 다른 좌표계는 다음 기회에 공부 후 정리하겠습니다.
- Haversine 공식은 구면 기하학에서 두 점 사이의 거리를 구하는 데 사용되는 공식입니다.
지구 역시 구형이며, 위에서 설명한 지리적 좌표계상의 위도 경도 좌표 데이터는 이를 기반으로 정의되었으므로,
지도상 두 좌표 간의 거리를 이 공식을 사용하여 구할 수 있습니다.
- 지도 좌표 2개 사이의 거리를 구하는 함수는 아래와 같이 구현합니다.
// (지도 좌표 1 에서 지도 좌표 2 까지의 거리 (미터) 반환, 하버사인 공식)
fun getDistanceMeterBetweenTwoLatLngCoordinate(
latlng1: Pair<Double, Double>,
latlng2: Pair<Double, Double>
): Double {
val r = 6371e3 // 지구 반지름 (미터 단위)
val lat1Rad = latlng1.first * PI / 180 // deg to rad
val lat2Rad = latlng2.first * PI / 180 // deg to rad
val deltaLat = (latlng2.first - latlng1.first) * PI / 180 // deg to rad
val deltaLon = (latlng2.second - latlng1.second) * PI / 180 // deg to rad
val a = sin(deltaLat / 2) * sin(deltaLat / 2) +
cos(lat1Rad) * cos(lat2Rad) *
sin(deltaLon / 2) * sin(deltaLon / 2)
val c = 2 * atan2(sqrt(a), sqrt(1 - a))
return r * c
}
위 코드는 거리를 계산할 두 좌표 변수를 받고, 거리를 미터 단위로 반환하는 예시입니다.
먼저,
지구 반지름을 6371km, 즉 6,371,000m(미터)로 정의합니다.
거리를 미터로 반환하기 위해 기본 단위를 미터로 맞춘 것입니다.
그리고 latlng1과 latlng2의 위도(lat1Rad, lat2Rad) 및 두 좌표의 위도와 경도의 차이값(deltaLat, deltaLon)을 구한 후,
이를 라디안 값으로 변환합니다. (라디안 변환 공식: (각도) * PI / 180)
바로 하버 사인 공식을 적용하는데,
먼저 a 값을 구합니다.
a = sin(deltaLat / 2)² + cos(lat1Rad) * cos(lat2Rad) * sin(deltaLon / 2)²
이는 두 위도와 경도의 차이에 대해 삼각함수를 적용한 값입니다.
다음으로 c 값을 구합니다.
c = 2 * atan2(sqrt(a), sqrt(1 - a))
c는 두 점 사이의 중심 각(라디안)을 구하는 것으로, Haversine 공식을 마무리하는 단계입니다.
마지막으로 r * c를 곱하여 두 점 사이의 거리를 미터 단위로 반환합니다. 여기서 r은 지구의 반지름(미터)이고, c는 중심 각도(라디안)입니다. 이를 곱하면 두 좌표 간의 곡면 거리가 나옵니다.
이제 이 함수를 실행해보고 실제로 테스트해보겠습니다.
테스트 방식은, 공신력 있는 구글 지도를 사용하여 먼저 두 좌표와 그 사이의 거리를 구한 후, 위에서 작성한 함수로 해당 좌표를 입력하여 동일한 거리가 나오는지 비교하는 방법을 사용할 것입니다.

처음 좌표는 37.544805, 126.887476 입니다.

다음 좌표는 37.463494, 127.039658 입니다.

두 위치의 거리를 재면, 대략 16.19KM(16190M), 가 나오게 됩니다. (마우스로 클릭하여 설정하였으므로 약간의 오차는 발생할 것입니다.)
fun api1GetDistanceMeterBetweenTwoCoordinate(
httpServletResponse: HttpServletResponse,
latitude1: Double,
longitude1: Double,
latitude2: Double,
longitude2: Double
): C9Service1TkV1MapCoordinateCalculationController.Api1GetDistanceMeterBetweenTwoCoordinateOutputVo? {
httpServletResponse.status = HttpStatus.OK.value()
return C9Service1TkV1MapCoordinateCalculationController.Api1GetDistanceMeterBetweenTwoCoordinateOutputVo(
MapCoordinateUtil.getDistanceMeterBetweenTwoLatLngCoordinate(
Pair(latitude1, longitude1),
Pair(latitude2, longitude2)
)
)
}
위와 같은 코드로 테스트를 해보면,
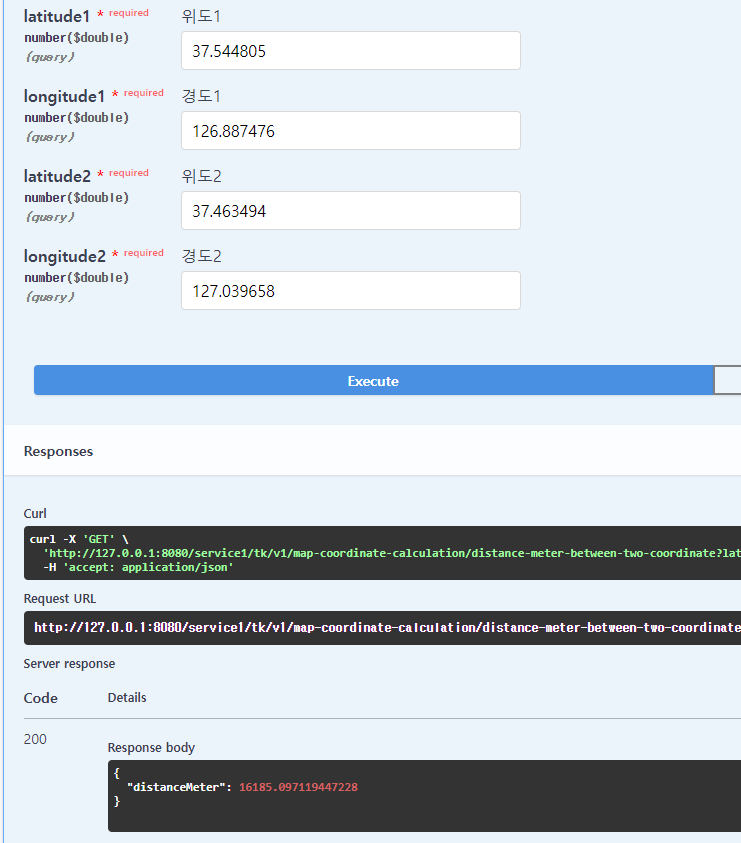
이처럼 허용될만한 오차범위(구글 맵 거리 계산시 클릭으로 좌표 아이콘 수정) 내에서 값이 반환되는 것을 볼 수 있습니다.
- 이상입니다.
이번에는 지리 정보에 대한 기본적인 지식을 습득하였고, HarverSine 공식을 사용하여 좌표간 거리를 측정해보았는데, 학문적인 내용을 계속 진행하면서, 좌표 거리 알고리즘을 보다 개선해 나갈 예정입니다.
위와 같은 방식으로 좌표간 거리를 구하는 것은 실질적으로 오차가 발생할 수 밖에 없는 방식입니다.
실제 지구는 타원형이지만, 하버사인 공식은 지구를 완전한 구형으로 가정하여 계산을 진행하기 때문입니다.
다음번 글에서는 Vincenty 공식과 같은 더 정확한 거리 계산이 가능한 공식을 도입하는 예시를 정리하겠습니다.
'Study > ETC' 카테고리의 다른 글
| [확률 통계] 표본 분산을 n-1로 나누는 이유 (구 블로그 글 복구) (0) | 2025.04.12 |
|---|---|
| [수학] 구면 삼각법의 이해, 증명, 응용 (0) | 2024.10.11 |
| [지리 정보] Vincenty 공식을 이용한 지도 좌표 거리 계산 및 Kotlin 함수 작성 (1) | 2024.10.09 |