- 구면 삼각법을 이해한다면 구체 위에서 일어나는 좌표의 움직임을 수학적으로 계산할 능력을 갖추게 될 것입니다.
지리정보 혹은 3차원 정보처리 등에 사용되는 원리를 이해하는데에 큰 도움이 되는 지식입니다.
이번 포스팅에서는 기초 삼각법에서 시작하여 구면 삼각법 까지를 정리하겠습니다.
모르시는 내용이라면 아래에 저와 같이 공부하시면 되고, 아시는 내용이시라면 빠르게 넘어가며 이해하도록 합시다.
- 차례대로 설명을 시작하겠습니다.
(삼각형의 성질과 삼각비)
1. 삼각형의 기본 성질
먼저 우리가 다루려는 삼각형의 성질에 대해 이해가 필요합니다.
삼각형은 세 변과 세 각으로 이루어진 다각형으로, 각 변의 길이와 각도 간에는 몇 가지 중요한 관계가 있습니다.
삼각형의 각도 합
삼각형 내부의 세 각의 합은 항상 180도입니다. 이 성질은 어떤 종류의 삼각형이든지 항상 성립합니다.
예를 들어, 한 삼각형의 두 각이 각각 60도와 80도일 때, 나머지 한 각은:
180 - (60+80) = 40
따라서 나머지 각은 40도입니다.
삼각형의 불등식
삼각형의 세 변의 길이에는 중요한 관계가 있습니다. 어느 두 변의 길이의 합은 항상 나머지 한 변의 길이보다 큽니다. 이를 삼각형의 불등식이라 부릅니다.
만약 삼각형의 세 변이 각각
a, b, c라면, 다음이 성립합니다:
a+b>c, a+c>b, b+c>a
삼각형의 종류
삼각형은 변의 길이와 각도에 따라 여러 가지로 분류됩니다:
정삼각형: 세 변의 길이가 같고, 각도는 모두 60도입니다.
이등변삼각형: 두 변의 길이가 같고, 두 각이 동일합니다.
직각삼각형: 한 각이 90도인 삼각형입니다.
둔각삼각형: 한 각이 90도보다 큰 삼각형입니다.
예각삼각형: 세 각이 모두 90도보다 작은 삼각형입니다.
2. 삼각비 (Trigonometric Ratios)
삼각비는 직각 삼각형의 각도와 변의 비율을 설명하는 개념입니다. 삼각비는 세 가지 중요한 함수로 나뉩니다:
사인(Sin), 코사인(Cos), 탄젠트(Tan).
삼각비는 삼각함수의 기초가 됩니다.
사인(Sine, Sin)
직각삼각형에서 한 각도(직각의 점과 더불어 밑변을 이루는 점의 각도)를 θ라 할 때, 그 각도의 사인 값은 다음과 같이 정의됩니다:
sin𝜃 =높이 / 빗변
높이: 직각을 이루는 두 변 중 하나, 각도 θ에 대응하는 변.
빗변: 직각을 마주보는 변.
코사인(Cosine, Cos)
cos𝜃=밑변 / 빗변
밑변: 각도 θ와 접한 변.
빗변: 직각을 마주보는 변.
탄젠트(Tangent, Tan)
tan𝜃=높이/밑변
탄젠트는 높이와 밑변의 비율로 나타내집니다.
삼각비 표
각각의 삼각비 값은 각도에 따라 달라지며, 각도를 기준으로 사인, 코사인, 탄젠트 값을 구하는 데 사용됩니다. 30도, 45도, 60도의 삼각비는 자주 사용되는 값입니다:

3. 삼각비의 활용
삼각비는 삼각형에서 변의 길이를 구하거나 각도를 계산하는 데 매우 유용합니다.
예시 1: 높이 구하기
어느 건물의 높이를 측정하려 합니다. 50m 떨어진 곳에서 건물을 봤을 때 시선과 지면이 이루는 각도가 30도입니다. 이때 건물의 높이를 구해보세요.
각도 θ=30∘, 밑변(거리가) 50m, 건물 높이 h.
tanθ= h / 50, 따라서 h=50×tan30∘
tan30∘ = 1/sqrt(3), 따라서 h=50× 1/sqrt(3) ≈ 28.87m.
건물의 높이는 약 28.87m입니다.
예시 2: 빗변 구하기
사다리의 한 끝이 벽에 놓여 있고, 벽에서의 높이가 4m, 사다리와 바닥이 이루는 각이 60도입니다. 사다리의 길이를 구해보세요.
각도 𝜃=60∘, 높이 4m, 빗변 c.
sinθ= 4/c, 따라서 c= 4/sin 60 ∘
sin 60 ∘ = sqrt(3)/2, 따라서 c = 4/ sqrt(3)/2 = 8/sqrt(3) ≈4.62m.
사다리의 길이는 약 4.62m입니다.
4. 삼각비의 확장
삼각비는 직각삼각형 외에도 임의의 삼각형에서도 적용할 수 있습니다. 이때 사인 법칙과 코사인 법칙을 사용합니다.
(사인 법칙과 코사인 법칙)
1. 사인 법칙 (Law of Sines)
사인 법칙은 삼각형의 두 변과 그에 대응하는 각도를 이용해 나머지 변이나 각도를 구할 수 있는 법칙입니다. 특히, 직각삼각형이 아닌 일반 삼각형에서 유용합니다.
사인 법칙의 공식
삼각형 ABC에서 각 A, B, C에 대응하는 변의 길이를 각각 a, b, c라 할 때, 다음과 같은 관계가 성립합니다:
a / sin(A) = b / sin(B) = c / sin(C)
sin(A) / a = sin(B) / b = sin(C) / c
설명
a: 각 A에 대응하는 변.
b: 각 B에 대응하는 변.
c: 각 C에 대응하는 변.
사인 법칙은 세 각도의 사인 값과 대응하는 변의 비율이 모두 같다는 것을 의미합니다.
사인 법칙의 활용
위와 같은 규칙이 왜 성립되는지에 대한 이해는 여기서 파고들지 맙시다.
저러한 법칙이 수학적으로 성립되기에, 앞으로는 위 법칙을 활용하여 수학적 답을 찾아내는 도구로 사용하면 되는 것입니다.(수학에는 이해력도 중요하지만, 문제 파악 능력과 기억력과 응용력 또한 높게 요구되는 것 같습니다.)
사인 법칙은 각도와 변의 길이를 구할 때 사용될 수 있으며, 삼각형의 두 각과 한 변의 길이를 알고 있을 때 나머지 변이나 각을 구하는 데 사용됩니다.
예시 문제
삼각형 ABC에서
∠A=30 ∘, ∠B=45 ∘, 그리고 변 a=10m일 때, 변 b의 길이를 구해보세요.
1. 먼저, 삼각형의 세 각의 합이 180도이므로:
∠C=180 ∘ −(30 ∘ +45 ∘)=105 ∘
2. 사인 법칙을 이용하면:
a / sin(A) = b / sin(B)
즉,
10/sin(30) = b / sin(45)
3. sin30 ∘ =0.5, sin45 ∘ = sqrt(2) / 2 이므로:
10 / 0.5 = b / sqrt(2) / 2
4. 양변을 풀면:
20 = b / sqrt(2) / 2 => b = 20 x sqrt(2) / 2 ≈14.14
따라서, 변 b의 길이는 약 14.14m입니다.
2. 코사인 법칙 (Law of Cosines)
코사인 법칙은 삼각형의 세 변의 길이와 한 각도 사이의 관계를 설명하는 법칙으로, 삼각형의 세 변 중 두 변과 그 사이의 각도를 알고 있을 때 나머지 변을 구하는 데 사용됩니다.
코사인 법칙의 공식
삼각형 ABC에서 각 A에 대응하는 변을 a, 각 B에 대응하는 변을 b, 각 C에 대응하는 변을 c라 할 때, 다음과 같은 공식이 성립합니다:
a^2 = b^2 + c^2 - 2bc * cos(A)
b^2 = a^2 + c^2 - 2ac * cos(B)
c^2 = a^2 + b^2 - 2ab * cos(C)
cos(A) = (b^2 + c^2 - a^2) / 2bc
cos(B) = (a^2 + c^2 - b^2) / 2ac
cos(C) = (a^2 + b^2 - c^2) / 2ab
설명
이 공식은 두 변의 길이와 그 사이의 각도를 알 때 나머지 변의 길이를 구하는 데 사용됩니다.
또한, 삼각형의 세 변의 길이를 알면 각도를 구할 때도 사용됩니다.
코사인 법칙의 활용
변을 구할 때: 삼각형의 두 변과 그 사이의 각도를 알고 있을 때 나머지 변을 구할 수 있습니다.
각도를 구할 때: 삼각형의 세 변을 알고 있을 때, 각도를 구하는 데 사용됩니다.
예시 문제
삼각형 ABC에서 변 b=8m, c=10m, 그리고 각 A=60 ∘ 일 때, 변 a의 길이를 구해보세요.
1. 코사인 법칙을 사용하여:
a^2 = b^2 + c^2 - 2bc * cos(A)
값을 대입하면:
a^2 = 8^2 + 10^2 - 2*8*10*cos(60)
2. cos60 ∘ =0.5이므로:
a^2 = 64 + 100 - 160 * 0.5
a^2 = 164 - 80 = 84
3. 따라서:
a = sqrt(84) ≈ 9.17
변 a의 길이는 약 9.17m입니다.
3. 사인 법칙과 코사인 법칙의 차이
사인 법칙은 주로 "두 각과 한 변의 길이를 알고 있을 때 나머지 변이나 각도를 구하는 데 사용"됩니다.
코사인 법칙은 "두 변과 그 사이의 각도를 알 때, 나머지 변을 구하거나, 세 변의 길이를 알 때 각도를 구하는 데 사용"됩니다.
4. 사인 법칙과 코사인 법칙의 활용 상황
사인 법칙은 삼각형이 직각이 아닌 상황에서도 비교적 쉽게 사용할 수 있습니다.
코사인 법칙은 두 변과 그 사이의 각도를 알 때, 삼각형의 나머지 정보를 계산할 수 있어 매우 유용합니다.
(구면 삼각법의 이해)
- 구면 삼각법은 구(球) 표면에서 이루어진 삼각형을 다루는 수학으로, 지리학, 천문학, 항해 등 여러 분야에서 중요하게 사용됩니다.
1. 구면 삼각형이란?
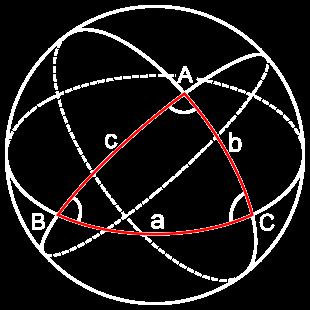
구면 삼각형은 구의 표면 위에서 세 개의 큰 원(대원 : 지구의 경도나 위도선처럼, 구의 중심을 지나는 원, 구의 중심을 지나지 않는 구 내부의 원을 작은 원, 즉 소원이라 합니다.)이 만들어내는 삼각형을 말합니다. 구면 삼각형은 평면 삼각형과는 몇 가지 중요한 차이점이 있습니다.
구면 삼각형의 특징
구면 삼각형의 변은 직선이 아닌 곡선으로, 구 표면의 큰 원의 호로 이루어져 있습니다.
구면 삼각형의 각도 합은 180도보다 큽니다. 일반적으로 180도에서 540도 사이의 값을 가집니다.
구면 삼각형의 각도는 평면에서의 각도와 다르게 구의 중심에서 각 변이 이루는 각도에 의해 결정됩니다.
(위 그림에서 a, b, c 로 이루어진 선을 보면, 구면 내의 원의 호의 결합으로 이루어져 있음을 알 수 있습니다. 해당 원은 구의 상하를 가르는 원과 좌우를 가르는 원을 기준으로 한 각도로 결정됩니다.)

2. 구면 좌표계(Spherical Coordinates)
구면 삼각법을 이해하기 위해서는 먼저 구면 좌표계를 알아야 합니다. 구면 좌표계는 구의 표면 위의 점을 반지름, 극각(경도), 방위각(위도)을 이용해 나타냅니다.
반지름: 구의 중심에서 표면 위의 한 점까지의 거리입니다.
극각(경도): 구의 중심에서 표면을 기준으로 좌우로 회전한 각도입니다.
방위각(위도): 구의 표면 위에서 한 점이 적도와 이루는 각도입니다.
자세한 설명은 이 글을 참고하세요.
3. 구면 삼각법의 기초 법칙

구면 삼각법의 중요한 법칙은 평면 삼각법에서 사용되는 사인 법칙과 코사인 법칙의 구면 버전입니다.
구면 사인 법칙 (Spherical Law of Sines)
구면 사인 법칙은 다음과 같이 주어집니다:
sin a / sin A = sin b / sin B = sin c / sin C
sin A / sin a = sin B / sin b = sin C / sin c
여기서 :
A, B, C 는 삼각형의 세 각
a, b, c 는 각각 각에 대응하는 구면 삼각형의 변(구의 중심에서 변이 형성하는 중심각)
이 법칙은 구면 삼각형에서도 각과 변 사이의 비율이 일정하다는 것을 나타냅니다.
위 그림을 보고 설명하겠습니다.
a 각은 A 와 마주보며(a 가 커지면 A 도 커짐), a 가 속한 삼각형은 O E F 입니다.
(E 와 F 는 대충 B 와 C 안에 포함되도록 길이를 설정한 것입니다.)
sin a = FE / OE
이제 A 각을 알아야 하는데,
A 각을 지닌 삼각형을 a 에서 사용한 삼각형과 동일한 위치(O 에서 시작되는 동일한 길이를 가짐)에 놓아,
위 그림에서 보듯 E 에서 OA 로 직각으로 내려오는 D 라는 점을 만들고, D 에서 OAC 평면으로 직각으로 뻗어나가는 선을 그었으며 이를 E 에서 OAC 평면으로 직각으로 내려오는 직선과 만나게 하여 G 를 만들었고, 이로써 EDG 라는 삼각형을 만들었습니다.
sin A = E G / D E 입니다.
이제 구면 사인 공식을 증명하기 위하여 C 와 c 를 알아보자면,
sin a / sin A = F E / O E * D E / E G
이며,
sin c / sin C = D E / O E * F E / E G
로, 두 결과가 같으므로 구면 삼각형의 사인 법칙이 성립됨을 증명할 수 있습니다.
구면 코사인 법칙 (Spherical Law of Cosines)

구면 삼각형에서 코사인 법칙은 다음과 같습니다:
cos a=cos b ⋅ cos c + sin b ⋅ sin c ⋅ cos A
cos b=cos a ⋅ cos c + sin a ⋅ sin c ⋅ cos B
cos c=cos a ⋅ cos b + sin a ⋅ sin b ⋅ cos C
이 공식은 평면 삼각형의 코사인 법칙과 유사하지만, 구면에서의 변의 길이가 호의 길이로 표현된다는 점에서 차이가 있습니다.
다시 위 그림을 보며 설명하면,
각 b 를 사용하는 DOF 라는 삼각형과, 각 B 를 투영한 DHF 라는 빨간 삼각형이 있습니다.
둘 모두 DF 라는 선을 공유한다는 공통점이 있습니다.
DHF 삼각형에서 기본 코사인 법칙을 사용하면, DF^2 = DH^2 + FH^2 - 2DH * FH * cos B
DOF 삼각형에서 기본 코사인 법칙을 사용하면, DF^2 = OD^2 + OF^2 - 2OD * OF * cos b
라고 구할 수 있습니다.
DF^2 가 동일하므로,
DF^2
= DH^2 + FH^2 - 2DH * FH * cos B
= OD^2 + OF^2 - 2OD * OF * cos b
이렇게 정리됩니다.
DH^2 + FH^2 - 2DH * FH * cos B = OD^2 + OF^2 - 2OD * OF * cos b
=> FH^2 - 2DH * FH * cos B = (OD^2 - DH^2) + OF^2 - 2OD * OF * cos b
=> - 2DH * FH * cos B = (OD^2 - DH^2) + (OF^2 - FH^2 ) - 2OD * OF * cos b
=> 2OD * OF * cos b - 2DH * FH * cos B = (OD^2 - DH^2) + (OF^2 - FH^2 )
=> 2OD * OF * cos b = (OD^2 - DH^2) + (OF^2 - FH^2 ) + 2DH * FH * cos B
이때, 삼각형 OHD 와 삼각형 OHF 는 직각 삼각형이므로, 피타고라스 정리에 의해 다음을 만족합니다.
OD^2 = OH^2 + DH^2
OF^2 = OH ^2 + FH^2
피타고라스 정리를 사용하여 변을 소거하면
2OD * OF * cos b = (OD^2 - DH^2) + (OF^2 - FH^2 ) + 2DH * FH * cos B
=> 2OD * OF * cos b = ( (OH^2 + DH^2) - DH^2) + (( OH ^2 + FH^2 ) - FH^2 ) + 2DH * FH * cos B
=> 2OD * OF * cos b = 2OH^2 + 2DH * FH * cos B
=> OD * OF * cos b = OH^2 + DH * FH * cos B
=> cos b = OH / OD * OH / OF + DH / OD * FH / OF * cos B
로 정리되며,
직각 삼각형인 삼각형 OHD 와 삼각형 OHF 의 삼각비를 정리하면,
sin a = FH / OF
sin c = DH / OD
cos a = OH / OF
cos c = OH / OD
이므로,
이를 위 식에 대입하면,
cos b=cos a ⋅ cos c + sin a ⋅ sin c ⋅ cos B
위와 같이 최종 답이 도출되어 구면 삼각형의 코사인 법칙이 올바르다는 것을 증명해내었습니다.
4. 구면 삼각법의 활용
구면 삼각법은 평면 삼각법과 달리 3 차원 공간에서 구의 형태를 지니는 지구의 곡면을 다룰 때 매우 유용합니다. 구면 삼각형의 각 변과 각도를 통해 위치, 방향, 거리 등을 계산할 수 있습니다.
항해와 지도 제작
구면 삼각법은 항해에서 두 지점 사이의 최단 경로(대원 경로)를 찾는 데 필수적입니다. 예를 들어, 두 도시의 위도와 경도를 알면 구면 삼각법을 이용해 그 사이의 거리를 계산할 수 있습니다.
천문학
천문학에서도 구면 삼각법이 필수적입니다. 하늘의 별과 행성들의 위치를 구할 때, 천체의 구면 좌표계에서 삼각법을 사용하여 그 위치를 계산합니다.
5. 추가로 구면 삼각형에서의 면적을 구하는 공식입니다.
구면 삼각형의 면적 공식
구면 삼각형의 면적은 다음과 같은 공식을 이용해 계산됩니다:
면적=E×r^2
여기서,
E는 여분각(excess angle)으로, 구면 삼각형의 세 각의 합에서 180도를 뺀 값입니다.(구면 삼각형 세 각의 합은 180도를 넘어감)
즉, E=(∠A+∠B+∠C)−180 ∘
r은 구의 반지름으로, 이 값을 구의 반지름의 제곱에 곱하면 면적을 구할 수 있습니다.
예시 문제
구면 삼각형 ABC에서 각 A, B, C가 각각 80도, 70도, 60도일 때, 구의 반지름이 6371km(지구의 반지름)라고 하면 이 삼각형의 면적을 구해보겠습니다.
∠A+∠B+∠C=80 ∘ +70 ∘ +60 ∘ =210 ∘
E=210 ∘ −180 ∘ =30 ∘
따라서 면적은:
30 ∘ ×( π /180 ∘ ) × 6371^2
(라디안으로 변환하였습니다.)
대략적으로 계산하면:
면적≈0.5236×6371^2 ≈212,000km^2
6. 마지막으로, 구면 삼각법을 사용한 응용 문제를 풀어보고 마치겠습니다.
문제 1) 지구상 좌표 사이의 거리 구하기
구면 삼각법의 대표적인 실전 문제 중 하나는, 지구 표면 위의 두 도시 사이의 최단 거리를 구하는 문제입니다. 지구는 구형에 가까운 모양이기 때문에 평면 삼각법이 아니라 구면 삼각법을 사용해야 정확한 거리를 계산할 수 있습니다.
문제
뉴욕(위도: 40.7128° N, 경도: 74.0060° W)과 도쿄(위도: 35.6895° N, 경도: 139.6917° E) 사이의 최단 거리를 구하세요. 지구의 반지름을 6371km로 가정합니다.
해결 방법
먼저 각 도시의 위도와 경도를 라디안으로 변환해야 합니다.
뉴욕의 위도와 경도는
40.7128 ∘ N과 74.0060 ∘ W, 도쿄의 위도와 경도는 35.6895 ∘ N과 139.6917 ∘ E입니다.
뉴욕의 위도 (라디안) = 40.7128 ∘ × π /180 ∘ = 0.7106라디안
뉴욕의 경도 (라디안) = 74.0060 ∘ × π /180 ∘ = 1.2916라디안
도쿄의 위도 (라디안) = 35.6895 ∘ × π /180 ∘ = 0.6229라디안
도쿄의 경도 (라디안) = 139.6917 ∘ × π /180 ∘ =2.4381라디안
다음으로, 구면 코사인 법칙은 두 지점 사이의 각도 c를 구하는 데 사용할 수 있습니다.
공식은 다음과 같습니다:
cos 𝑐 = sin(lat1) ⋅ sin(lat2) + cos(lat1) ⋅ cos(lat2) ⋅ cos(long1−long2)
위 수식은 구면 코사인 법칙을 변경한 것입니다. (변경 방식은 나중에 정리하겠습니다.)
여기에 뉴욕과 도쿄의 좌표를 대입하면:
cos c = sin(0.7106) ⋅ sin(0.6229) + cos(0.7106) ⋅ cos(0.6229) ⋅ cos(1.2916−2.4381)
계산을 하면:
cosc≈0.6521
따라서:
c=cos ^ −1(0.6521)≈0.8649라디안
거리를 계산 두 도시 사이의 거리 d는 각도 c와 지구의 반지름 r=6371km를 곱하여 구합니다:
d=6371×0.8649≈5508km
계산 결과 뉴욕과 도쿄 사이의 최단 거리는 약 5508km입니다.
문제 2) 구면 삼각형에서의 각도 구하기
구면 삼각법을 사용한 대표적인 문제 유형은 앞서 보았듯 두 좌표를 통해 거리를 구하는 것이 있고, 또 하나는 두 변이 주어졌을 때, 세 번째 변의 각도를 구하는 문제가 있습니다.
문제 2 에서 알아볼 각도 구하기 문제는 항해나 천문학에서 특정 지점의 방향을 계산하는 데 유용합니다.
문제
구면 삼각형에서 두 변
a=60 ∘ , b=70 ∘ 이고, 그 사이의 각 C=45 ∘ 일 때, 나머지 각도 A를 구하세요.
해결 방법
구면 코사인 법칙을 사용하여 각 A를 구할 수 있습니다.
공식은:
cos A= (cos a−cos b⋅cos c) / (sin b ⋅ sin c)
여기서, 각 c는 주어지지 않았으므로 구면 코사인 법칙을 한 번 더 사용해 구할 수 있습니다:
cos c = cos a ⋅ cos b + sin a ⋅ sin b ⋅ cos C
먼저 c를 구해보면:
cos c = cos60 ∘ ⋅cos70 ∘ + sin60 ∘ ⋅sin70 ∘ ⋅cos45 ∘
계산하면:
cos c ≈ 0.7641
따라서
c ≈ cos ^−1 (0.7641) ≈ 40.64 ∘
이제 구면 코사인 법칙을 다시 사용하여 각 A를 구하면:
cos A = (cos60 ∘ −cos70 ∘ ⋅ cos40.64 ∘) / (sin70 ∘ ⋅sin40.64 ∘)
계산하면:
cos A ≈ 0.7486
따라서:
A = cos ^−1 (0.7486) ≈ 41.41 ∘
계산 결과 구면 삼각형에서 각도 A는 약 41.41도입니다.
- 이상입니다.
'Study > ETC' 카테고리의 다른 글
| [확률 통계] 표본 분산을 n-1로 나누는 이유 (구 블로그 글 복구) (0) | 2025.04.12 |
|---|---|
| [지리 정보] Vincenty 공식을 이용한 지도 좌표 거리 계산 및 Kotlin 함수 작성 (1) | 2024.10.09 |
| [지리 정보] 지리적 좌표계, 위도/경도의 이해 및 Haversine 공식을 이용한 지도 좌표 거리 계산 Kotlin 함수 작성 (2) | 2024.10.08 |
